August 2019 archive
Saturday 31 Aug 2019 comment?


I
walked past this rabbit today and he hid under an
upside‑down wheelbarrow.
He's a youngster, perhaps not experienced
enough to know how readily he can run away from big slow bipeds.
I figured he'd come out once the coast was clear
but he hung out there for several hours. It was,
after all, a shady spot.
Thursday 29 Aug 2019 1 comment


 Above: back cover of a road map from 1967,
when gas stations gave them away.
Above: back cover of a road map from 1967,
when gas stations gave them away.
Right: back cover of Mad #92, January 1965. |
Monday 26 Aug 2019 comment?
These things happened today:
These things happened today:
- The NY Times sent out a memo to its employees warning them of bedbugs in the company's headquarters building.
- Stuart A. Thompson, who works at the Times, tweeted about the bedbugs in the Times' newsroom.
- David Karpf
(Associate Professor in the School of Media and
Public Affairs at George Washington University) responded with
a tweet metaphorically
equating a NY Times columnist he's not keen on
(Bret Stephens) to the bedbugs:

- Way before that tweet got
much attention, Bret Stephens
emailed
Professor Karpf to tell him what he thought of it:
Dear Dr. Karpf,
...and cc-ed his email to Professor Karpf's provost at GWU.
Someone just pointed out a tweet your wrote about me, calling me a "bedbug." I'm often amazed about the things supposedly decent people are prepared to say about other people -- people they've never met -- on Twitter. I think you've set a new standard. ... - Something akin to the Streisand effect kicked in. Bret Stephens' Wikipedia page got vandalized to say "Bret Bedbug Stephens", among other things. The vandalism has since been reverted and his Wikipedia page is locked down for now. Other humor at the expense of Bret Stephens ensued on Twitter.
Saturday 24 Aug 2019 comment?
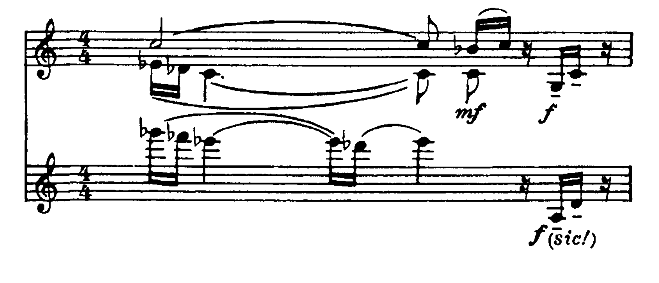 An excerpt
from the first movement of Contrasts by Béla Bartók.
The upper staff is the violin part (non-transposing); the lower staff
is for clarinet in A (sounds a minor third lower than notated).
An excerpt
from the first movement of Contrasts by Béla Bartók.
The upper staff is the violin part (non-transposing); the lower staff
is for clarinet in A (sounds a minor third lower than notated).
I like the (sic!) which seems to be telling the clarinetist: not a typo!—despite how dolce the rest of this passage was, this pair of notes really is one semitone lower than what the violin is playing.
 An excerpt
from the first movement of Contrasts by Béla Bartók.
The upper staff is the violin part (non-transposing); the lower staff
is for clarinet in A (sounds a minor third lower than notated).
An excerpt
from the first movement of Contrasts by Béla Bartók.
The upper staff is the violin part (non-transposing); the lower staff
is for clarinet in A (sounds a minor third lower than notated).
I like the (sic!) which seems to be telling the clarinetist: not a typo!—despite how dolce the rest of this passage was, this pair of notes really is one semitone lower than what the violin is playing.
Wednesday 14 Aug 2019 comment?


Roadrunner
from yesterday morning.
This one doesn't have its crest raised like most of the ones in pics I've posted before—kind of like the jackrabbit a couple weeks ago whoseradiators ears weren't raised.
This one doesn't have its crest raised like most of the ones in pics I've posted before—kind of like the jackrabbit a couple weeks ago whose
Saturday 10 Aug 2019 2 comments
Beware: math-intensive posting today.
The Wikipedia Vector space article gives the complex numbers as an example of a vector space over the reals and notes that it's isomorphic to the vector space of ordered pairs of real numbers. That's straightforward; what follows is less obvious.
Consider the real numbers as a vector space over the rationals. A theorem that follows from the Axiom of Choice says that every vector space has a basis, thus this vector space does. Call such a basis B. B is an infinite set with the same cardinality as ℝ.
Consider the set of all ordered pairs (b₁,0) where b₁∈B or (0,b₂) where b₂∈B; call this set BB. That is, BB = (B×{0}) ∪ ({0}×B). BB also has the same cardinality as ℝ and can be put into a one‑to‑one correspondence with B.
With b₁ and b₂ interpreted as coefficients of 1 and i respectively, BB is a basis for the vector space of complex numbers over the rationals.
A one‑to‑one correspondence between B and BB induces an isomorphism between their respective vector spaces. Thus the group (ℝ,+) is isomorphic to the group (ℂ,+). This is one of my favorite counterintuitive consequences of the Axiom of Choice.
followup, 24-jan-24: more detailed proof available as PDF
Beware: math-intensive posting today.
The Wikipedia Vector space article gives the complex numbers as an example of a vector space over the reals and notes that it's isomorphic to the vector space of ordered pairs of real numbers. That's straightforward; what follows is less obvious.
Consider the real numbers as a vector space over the rationals. A theorem that follows from the Axiom of Choice says that every vector space has a basis, thus this vector space does. Call such a basis B. B is an infinite set with the same cardinality as ℝ.
Consider the set of all ordered pairs (b₁,0) where b₁∈B or (0,b₂) where b₂∈B; call this set BB. That is, BB = (B×{0}) ∪ ({0}×B). BB also has the same cardinality as ℝ and can be put into a one‑to‑one correspondence with B.
With b₁ and b₂ interpreted as coefficients of 1 and i respectively, BB is a basis for the vector space of complex numbers over the rationals.
A one‑to‑one correspondence between B and BB induces an isomorphism between their respective vector spaces. Thus the group (ℝ,+) is isomorphic to the group (ℂ,+). This is one of my favorite counterintuitive consequences of the Axiom of Choice.
followup, 24-jan-24: more detailed proof available as PDF
Saturday 03 Aug 2019 comment?
I like
The Counselor (2013).
 34% on Rotten Tomatoes.
34% on Rotten Tomatoes.
| current xkcd: |  |
 34% on Rotten Tomatoes.
34% on Rotten Tomatoes.
xkcd #2184
by Randall Munroe used here
by kind permission under license
(CC BY-NC 2.5)
/ converted to indexed PNG
current journal
FAQ
search
contact
rss/xml
atom/xml
spam notice
terms of use
warrant canary
archive
FAQ
search
contact
rss/xml
atom/xml
spam notice
terms of use
warrant canary
archive
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |