A couple years ago, two eminent mathematicians published a paper, The Free Will Theorem, which starts with this paragraph:

Do we really have free will, or, as a few determined folk maintain, is it all an illusion? We don’t know, but will prove in this paper that if indeed there exist any experimenters with a modicum of free will, then elementary particles must have their own share of this valuable commodity.

Although most of the material in the paper isn't new, it's a creditable exercise in deducing their result from a minimal set of axioms. It's written in the accessible, playful style that one of its authors (John Horton Conway) is known for.

Readers have generally found the paper's math and physics to be unobjectionable, but questions remain about its philosophical aspects. The argument may be sound, but its applicability is subject to interpretation.

The paper emphasize the importance of will ("free will moves mountains"), but it sidesteps the issue of what determinism has to do with the subjective and practical aspects of will. Admittedly this is a can of worms, and I can see why the scope of the paper is limited. In my opinion, though, many of the most interesting questions about free will lie in just those areas that the paper avoids.

From the paper's philosophical remarks:

It follows that we cannot prove our Free Will assumption--determinism, like solipsism, is logically possible. Both the non-existence of free agents in determism and the external world in solipsism are rightly conjured up by philosophers as consistent if unbelievable universes to show the limits of what is possible, but we discard them as serious views of our universe.

It is hard to take science seriously in a universe that in fact controls all the choices experimenters think they make. Nature could be in an insidious conspiracy to "confirm" laws by denying us the freedom to make the tests that would refute them. Physical induction, the primary tool of science, disappears if we are denied access to random samples. It is also hard to take seriously the arguments of those who according to their own beliefs are deterministic automata!

I find that last remark especially unconvincing, and a bit of a cheap shot. Arguments should stand or fall on their merits alone.

The subject of will means a lot to me. The study of will touches on interesting issues in neuroscience, psychology, ethics, and yes, even math and physics. But--as is my wont--I try not to get attached to one belief or another. Beliefs are models, and are thus limited and provisional. When all is said and done, will and initiative remain worth cultivating at a practical level.

From an article in yesterday's NY Times about browsers:

But the new version should prompt everyone who has abandoned I.E. over the years to give it another look. It's speedy, it seems inured to crashes, and not only does it match its rivals' features--in some cases, I.E. beats them.

I'm skeptical that IE is advanced enough to have feelings (in this case, of being inured to crashes). If the author instead meant that the browser is modular and can tolerate subsystem failures without bringing down the whole browser, that's pleasant--but not well described by "it seems inured to crashes".

50 years ago.

Yesterday, the US House of Representatives passed this resolution:

Whereas the Greek letter (Pi) is the symbol for the ratio of the circumference of a circle to its diameter;

Whereas the ratio Pi is an irrational number, which will continue infinitely without repeating, and has been calculated to over one trillion digits;

[...]

Whereas Pi can be approximated as 3.14, and thus March 14, 2009, is an appropriate day for "National Pi Day": Now, therefore, be it

Resolved, That the House of Representatives--

(1) supports the designation of a "Pi Day" and its celebration around the world;

(2) recognizes the continuing importance of National Science Foundation's math and science education programs; and

(3) encourages schools and educators to observe the day with appropriate activities that teach students about Pi and engage them about the study of mathematics.

The resolution was adopted by a vote of 391 to 10. (All 10 nay votes were cast by Republicans, I assume dedicated to limiting government interference in our lives.)

Supporting the celebration of Pi Day on 3-14 "around the world" is a stretch, given that much of the world doesn't follow the convention of writing month before date.

It was windy this morning, lousy weather for walking--but a good morning for staying inside and taking apart a disk drive.

The drive I plundered today is 16 years old, thus bulkier and with more disk platters than typical current-day drives. But the general idea is the same: a machined aluminum case, disks stacked around a motor, and a pivoted arm driven by coils of wire in the field of neodymium magnets.

The magnets are worth keeping.

A 1985 map, and Google maps today: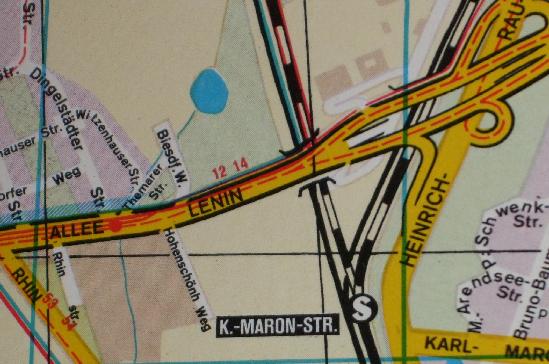

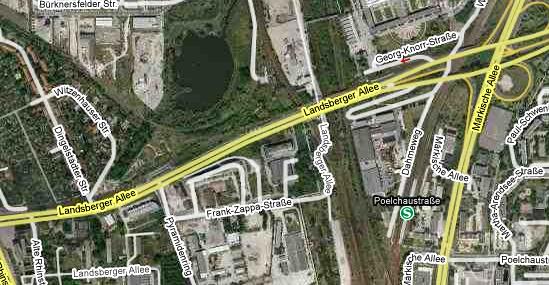
This is in what was East Berlin. Streets that the 1985 map shows as named after Lenin, Heinrich Rau, and Karl Maron have since been renamed.

The thin black lines on the 1985 map are a one-kilometer grid, noticeably curved on the full map because the scale varies continuously across the page (from 1:25000 for central Berlin to 1:35000 for the outskirts).

Another belated celebration:  yesterday was Dr. Seuss's birthday.

In 2007, a US Magistrate Judge in New Hampshire issued an order in verse inspired by Green Eggs and Ham. Seeing how far a Seuss-wannabe falls short is to be reminded of how skilled the Doctor was.

One more piece (already one too many, probably) of judicial poetry, from Michigan appeals judge J. H. Gillis:

We thought that we would never see
A suit to compensate a tree.

With the caveat that I may fail,
I will try to introduce a math topic in a way that's comprehensible and interesting to a lay reader.

Mathematics provides means for dealing with infinite sets: collections that can't be listed in full, yet can be defined and analyzed in a precise way. They're fun because they are often counterintuitive; they behave differently than more familiar finite sets.

To work with infinite sets--as with all formal mathematics--we need ground rules (axioms). My topic for today is a particular ground rule.

Imagine you have a number of bins, each containing one or more objects. Imagine you'd like a set of objects that's representative of all the bins: you want to pick one object from each bin. This is a trivial matter in finite cases--but if there are infinitely many bins, and no clear rule for how to pick an object from each bin, do we still deem it OK to talk about a set made by selecting one object from each bin?

There are lots of choices of ground rules. We can allow or disallow a rule and see what is and isn't possible in each case. (The option of Euclidean or non-Euclidean geometries is a classic instance of tinkering with a ground rule.)

Allowing selection from an infinite number of bins (known as the axiom of choice) has been studied at length. It turns out to be necessary for a lot of operations that mathematicians want to do, and it doesn't seem to be too much of a stretch--so what's not to like? I'll get to one of its gnarlier consequences in a moment, but first a caricature of mathematical stubbornness:

...we had better reject the axiom of choice on account of Murphy’s Law that 'if anything can go wrong, it will'. This is really no more than a personal hunch about the world of sets. We simply don't believe that there is a function that assigns to each non-empty set of real numbers one of its elements. ... And if you can't describe such a function, or even prove that it exists without using some relative of the axiom of choice, what makes you so sure there is such a thing?

[from tongue-in-cheek (?) remarks after a proof that isn't a joke]

I suckered you into reading this with the promise of something interesting, so here goes. It's been proven that if you allow the axiom of choice, you must live with the Banach-Tarski paradox: a 3-dimensional solid ball can be split into five pieces which can be moved and rotated and reassembled to make two identical copies of the original ball. Note that the axiom of choice doesn't tell you just what those five pieces are (although you can be sure they are intricate, bizarre sets of points). It only lets you prove that they can exist.

A proof of the Banach-Tarski paradox gets pretty involved. There are quite a few other consequences of the axiom of choice; if you'd be interested in one that's not too hard to follow, try the Vitali set.