Yesterday, I was chatting with a neighbor who owns a bar in Los Angeles. We compared notes about having been subject to attempted muggings on the street in L.A. .  In my case, assailants wanted my money. My neighbor thought the guys he encountered just wanted to beat him up and take his dog. Supposedly, robbing someone of their dog is a way to prove one's bad‑assedness to fellow gang members.

I said that I like living in Lone Pine. My neighbor asked if that incident changed my willingness to visit Los Angeles; I said no. It's not like it was the first urban skirmish I'd been through.

But I live where I do partly because people behave better here. I don't have to feel like I'm on my guard at all times. I've seen a nice car left running with the keys in it while someone went into the post office.

Or, as shown by this pic of a truck parked in town yesterday: you can expect your dog won't be stolen while you run errands.

Happy solstice (9:30 tonight, PST), everyone.

I texted a climbing buddy this morning to see if he was around, but alas no. His response said he was in other desert cities. That is, fate had taken him to that distinctive area east of one of my favorite road signs. Note also that California is such a high-tech state that we number our roads in binary.

photo by jfs1988; used by permission

The more humorous and/or outrageous a mnemonic is, the more easy it is to remember. The traditional and proposed mnemonics shown here are from xkcd. The ones I remember from school, e.g. "my very elegant mother just sat upon nine pancakes", are now obsolete in light of Pluto's demotion. The xkcd from which this is excerpted declines to note a traditional mnemonic for the resistor color code. The one I've heard the most over the years is crude: bad boys rape our young girls but violet goes willingly. If I had a Siri, I'd ask it why so much humor relies on cruelty.

xkcd graphic used by permission under CC BY-NC 2.5 license I've been avoiding blogging about current Republican candidates‑‑there are plenty of other places to go if you want to read about them‑‑but I make an exception today to revisit something I read some 15 years ago.

In addressing the question of where all the extra souls come from as human population expands, Ian Stevenson proposed that

... human minds may split or duplicate, so that one mind can reincarnate in two or more bodies; the Inuit, the Igbo of Nigeria, the Tibetans, the Haida of Alaska and British Columbia, and the Gitksan of British Columbia all believe this.¹

Paul Edwards' 1996 book on reincarnation quotes Stevenson and considers what it would mean if a split resulted in, say, a Newt Gingrich and a double thereof. A footnote says

For the benefit of readers in a happier time when Newt Gingrich will have been forgotten, let me explain that he was for several years after 1994 the Republican party's foremost spokesman for intolerance, divisiveness, narrow-mindedness, and contempt for the underdog.²

Gingrich remains a spokesman for all that, if perhaps not the party's foremost (competition is stiff). Consider that the USA now lets gay people serve openly in the military, the sky didn't fall as a result, and indeed most Americans now support the change; yet in an interview last week:

Interviewer:	Would you actively work to get [DADT] reinstated?
Gingrich:	Well, I would encourage the Congress to pass reinstating it, and I expect the next Congress will pass reinstating it.

The man is, as my boss would say, a specimen.

---

1	Children Who Remember Previous Lives, pp. 207-208
2	Reincarnation: A Critical Examination, pp. 230-231

Word is that someone recently said "cameras are not meant to be beautiful". Well. Anything with an infinity sign engraved on it should, as a matter of principle, be made so that it is beautiful. This of course exempts many modern-day cameras on which infinity is nowhere to be found.

The two puffs in the clouds are at two peaks in the ridge, almost as if the mountains pissed the clouds off at those points. It looks better embiggened (click on the image).

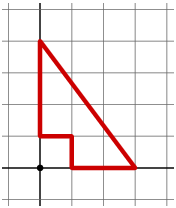A math problem from GCHQ: A polygon has vertices with integer coördinates (in 2 dimensions) and integer length edges. Show that the perimeter is an even integer. E.g., the red polygon in the diagram has a perimeter of 12.

The sides of the Great Pyramid of Giza are inclined at about 51.82° from horizontal. We do not know whether the designers were shooting for arctan(4/π) ≈ 51.854°, which would make the base's perimeter equal to the circumference of a circle whose radius was the pyramid's height. Nor do we know whether they had in mind arccos(Φ) ≈ 51.827°, which would make the area of each triangular face equal to the area of a square whose sides were the pyramid's height. (where uppercase Φ is the reciprocal of the golden ratio)

As the pyramid's base isn't a perfect square and the casing stones are missing, it's hopeless to try to resolve the question by measurement. It's down in the noise. That's not a bad thing at all, if you like mysteries.

Some historians say there's no evidence that the ancient Egyptians knew about the golden ratio. Maybe there's no evidence because they considered it a deep, dark secret. It's not a stretch to suppose that they held mathematics to have magical properties, as did the Pythagoreans later on.

In a modern instance of an urge to keep math secret, the MPAA sent letters demanding that web sites stop publishing the number 13,256,278,887,989,457,651,018,865,901,401,704,640. That led to it being published all over the place, an instance of the Streisand effect. And as long as we're on the topic of the MPAA, this is as good a time as any to say that This Film Is Not Yet Rated is worth seeing.

But back to the pyramid. It's a nice coïncidence that you can build something that's (even if unintentionally) so close to expressing either π or Φ that people will still be wondering about it 4550 years later. The near-equality at the heart of the matter can be simplified to π ≈ √(8√5 ‑ 8).

Almost-equalities, like lots of things, seldom have the cosmic significance people might want them to have. But they are occasionally useful. Equal temperament (more specifically, 12‑TET) exploits several near-equalities, e.g. 2^7/12 ≈ 3/2.