Tuesday 27 May 2014 1 comment
|
The only cactus I've had luck trying to grow from seed,
shown as a youngster here, here, and here, and which (so I hear) does not care about me, bloomed for the first time this morning. |
 |
Tuesday 20 May 2014 comment?
 Today's topic is the disposal of unwanted mattresses.
Today's topic is the disposal of unwanted mattresses.
I have no explanation for this pic other than to say that I took it in Los Angeles yesterday. I don't know what the author was sorry about. I hope they weren't apologizing in advance for their spray paint technique in this art installation, as I find the finished product quite satisfactory.
Around 24 years ago, a friend and I were in the process of disposing of a mattress. A bee somehow found its way underneath a plastic sheet the mattress was wrapped in; we left the mattress out on the sidewalk, giving the bee a chance to get free on its own before we came back in a few minutes with a truck.
We never found out what happened to the bee. Mattress, plastic sheet, and bee were all gone by the time we returned. Let the record show that it was my friend and not I who made the pun about mattress as bait in a sting operation.
Around 33 years ago I disposed of a mattress by leaving it on the roof of the apartment building I lived in. I figured someone would deal with it, which seems to have proved true: Google's aerial imagery shows no mattress-sized object on the roof.
I wouldn't leave a mattress on the roof of a building today. I offer the story as an instance of the type of youthful dopiness I sometimes exhibited. And if by a remarkable twist of fate that apartment building's manager is reading this: Forgive me—I'm sorry.
 Today's topic is the disposal of unwanted mattresses.
Today's topic is the disposal of unwanted mattresses.
I have no explanation for this pic other than to say that I took it in Los Angeles yesterday. I don't know what the author was sorry about. I hope they weren't apologizing in advance for their spray paint technique in this art installation, as I find the finished product quite satisfactory.
Around 24 years ago, a friend and I were in the process of disposing of a mattress. A bee somehow found its way underneath a plastic sheet the mattress was wrapped in; we left the mattress out on the sidewalk, giving the bee a chance to get free on its own before we came back in a few minutes with a truck.
We never found out what happened to the bee. Mattress, plastic sheet, and bee were all gone by the time we returned. Let the record show that it was my friend and not I who made the pun about mattress as bait in a sting operation.
Around 33 years ago I disposed of a mattress by leaving it on the roof of the apartment building I lived in. I figured someone would deal with it, which seems to have proved true: Google's aerial imagery shows no mattress-sized object on the roof.
I wouldn't leave a mattress on the roof of a building today. I offer the story as an instance of the type of youthful dopiness I sometimes exhibited. And if by a remarkable twist of fate that apartment building's manager is reading this: Forgive me—I'm sorry.
Thursday 15 May 2014 comment?
Glenn Greenwald was interviewed on NPR yesterday. At about a half hour into the programme, Terry Gross read Greenwald this paragraph from a review of his latest book, No Place To Hide :
But I found it strange that Professor Cole said there was nothing illegal about bugging embassies. It is contrary to the spirit and letter of the Vienna Convention on Diplomatic Relations, which the USA has ratified. (See article 22 in particular.) I exchanged email with Professor Cole about this, and he edited the online version of his book review to remove the words "illegal or".
I suggest that there are moral and political concerns about bugging embassies. Breaking treaties is dishonest, as is much of spying in general. Some may have made peace with that but it's still a moral question.
"... its disclosure ... is likely to cause serious diplomatic problems"— That is, it's bad for other countries to know what we're up to. Yet embassy bugging, the activity Professor Cole thinks is routine, is us doing whatever it takes to know what they are up to. The whole business is a huge double standard that you can tolerate only to the extent that you see foreign relations as law of the jungle—which of course it often is, but do we have to give up all aspiration of making it something better?
Germany in particular is exasperated, likening the USA to "cowboys who only understand the language of the Wild West". So yeah there have been serious diplomatic problems, but whose fault is that? Treating your allies as adversaries is asking for trouble.
That's not to say I disagree with all the points in David Cole's book review. He takes Greenwald to task for having a black and white view of things, and on this I think he has a point.
Glenn Greenwald was interviewed on NPR yesterday. At about a half hour into the programme, Terry Gross read Greenwald this paragraph from a review of his latest book, No Place To Hide :
Some disclosures raise more questions about Greenwald’s judgment than about the NSA’s activities. One document, for example, identifies the specific methods used to bug 24 named foreign embassies. The document reveals top-secret methods and targets, and its disclosure is likely to undermine legitimate intelligence-gathering and cause serious diplomatic problems. Yet it is difficult to see what possible value it adds to the public debate. It is one thing to disclose secret government practices that raise serious moral, political and constitutional concerns — as many of Snowden’s disclosures have done. But bugging foreign embassies is at the core of foreign intelligence, and there is nothing illegal or particularly surprising about the fact that we do it.The book review was by David Cole, a law professor who's litigated a number of civil liberties cases for which he has my respect. It's to the Washington Post's credit that they had Professor Cole write a critical review rather than someone thoroughly unsympathetic to any of Greenwald's points.
But I found it strange that Professor Cole said there was nothing illegal about bugging embassies. It is contrary to the spirit and letter of the Vienna Convention on Diplomatic Relations, which the USA has ratified. (See article 22 in particular.) I exchanged email with Professor Cole about this, and he edited the online version of his book review to remove the words "illegal or".
I suggest that there are moral and political concerns about bugging embassies. Breaking treaties is dishonest, as is much of spying in general. Some may have made peace with that but it's still a moral question.
"... its disclosure ... is likely to cause serious diplomatic problems"— That is, it's bad for other countries to know what we're up to. Yet embassy bugging, the activity Professor Cole thinks is routine, is us doing whatever it takes to know what they are up to. The whole business is a huge double standard that you can tolerate only to the extent that you see foreign relations as law of the jungle—which of course it often is, but do we have to give up all aspiration of making it something better?
Germany in particular is exasperated, likening the USA to "cowboys who only understand the language of the Wild West". So yeah there have been serious diplomatic problems, but whose fault is that? Treating your allies as adversaries is asking for trouble.
That's not to say I disagree with all the points in David Cole's book review. He takes Greenwald to task for having a black and white view of things, and on this I think he has a point.
Sunday 11 May 2014 comment?
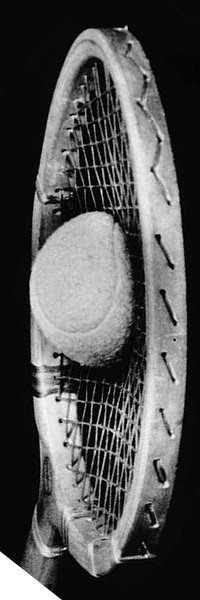 I would've liked to have met strobe photography pioneer Harold "Doc" Edgerton.
When someone asked him to photograph a bullet passing through a playing card,
he asked, "What part of the bullet? Front? Middle?"
I would've liked to have met strobe photography pioneer Harold "Doc" Edgerton.
When someone asked him to photograph a bullet passing through a playing card,
he asked, "What part of the bullet? Front? Middle?"
Word is that the guys at Los Alamos didn't have capacitors big enough to trigger the first atomic bomb and borrowed some from Edgerton. (Yes, I wonder how you "borrow" parts for an atomic bomb.) He not only gave them the capacitors, he designed a camera to take a pic of the explosion before it had spread to 100 yards wide. I got those anecdotes from a nice blog posting about Edgerton. It's from the house blog of a lens rental company, folks who have figured out themselves how to adjust various lens models because Leica, Nikon, et al. often don't publish repair manuals. Good blog if you like cameras. |
Thursday 08 May 2014 3 comments
Yesterday I read about a startup company offering forensic analysis to detect manipulated image files. They have a database of camera characteristics (e.g., sensor and software idiosyncrasies) and can test whether a JPEG file looks like it came directly out of the type of camera named in its metadata. Their free web-based photo analyzer went live this week.
Quite a few media outlets have parroted the company's press releases. Reporters were often too lazy to do even a casual experiment ("I uploaded a few photos and this is what their server said about them"). It takes all of one minute to submit an image file and get the analysis.
I uploaded two unaltered image files, one from a cellphone and one from a pocket digital camera, and the analysis failed to recognize them as originals. "Our forensic tests are inconclusive, so we are unable to confirm that this is an unmodified original file from a camera."
Try it yourself: www.izitru.com. For a photo to have a chance of being recognized as unaltered, it must be an original file from a digital camera, not cropped nor resized nor re-JPEG-compressed nor panorama-composited nor otherwise processed. I'd be interested to hear anyone's results.
My tests were just a small sample, but given the hype about "cutting-edge forensics" I was disappointed that Izitru had nothing to say about the kind of bona fide original photos that it's designed to be able to recognize. And I'm disappointed although not shocked by how journalists are happy to be little more than stenographers.
Yesterday I read about a startup company offering forensic analysis to detect manipulated image files. They have a database of camera characteristics (e.g., sensor and software idiosyncrasies) and can test whether a JPEG file looks like it came directly out of the type of camera named in its metadata. Their free web-based photo analyzer went live this week.
Quite a few media outlets have parroted the company's press releases. Reporters were often too lazy to do even a casual experiment ("I uploaded a few photos and this is what their server said about them"). It takes all of one minute to submit an image file and get the analysis.
I uploaded two unaltered image files, one from a cellphone and one from a pocket digital camera, and the analysis failed to recognize them as originals. "Our forensic tests are inconclusive, so we are unable to confirm that this is an unmodified original file from a camera."
Try it yourself: www.izitru.com. For a photo to have a chance of being recognized as unaltered, it must be an original file from a digital camera, not cropped nor resized nor re-JPEG-compressed nor panorama-composited nor otherwise processed. I'd be interested to hear anyone's results.
My tests were just a small sample, but given the hype about "cutting-edge forensics" I was disappointed that Izitru had nothing to say about the kind of bona fide original photos that it's designed to be able to recognize. And I'm disappointed although not shocked by how journalists are happy to be little more than stenographers.
Sunday 04 May 2014 2 comments
A while back, I wrote about the Banach-Tarski paradox: a decomposition of a sphere into parts that can be reassembled into two spheres.
I've since learned of another curious duplicating decomposition: the Sierpinski-Mazurkiewicz paradox, which I find even more remarkable in some aspects.
What it is: an infinite set of points S in the plane that can be divided into two subsets A and B, such that
S is the set of all polynomials with whole number (integer >= 0) coefficients, evaluated at q. Plot them as points on the complex plane. A few sample polynomials and their values at q:
Note that cos(1), sin(1), cos(2), sin(2), ... are all transcendental.
Partition S into two subsets:
Rotating the points in B clockwise by one radian (57.2957795...°) is tantamount to multiplying their values by e‑i, which reduces the exponent of each polynomial term by one. The result is all the points in S.
I don't know about you, but I think that's pretty cool.
Thanks to Dr. Francis Edward Su, on one of whose pages I found this.
To show that S is a countably infinite set, define the rank of each polynomial as its degree plus the sum of all its coefficients. E.g., the rank of x² + 3x is 2+1+3 = 6. To enumerate the polynomials with whole number coefficients,
There are finitely many polynomials of each rank.
A while back, I wrote about the Banach-Tarski paradox: a decomposition of a sphere into parts that can be reassembled into two spheres.
I've since learned of another curious duplicating decomposition: the Sierpinski-Mazurkiewicz paradox, which I find even more remarkable in some aspects.
What it is: an infinite set of points S in the plane that can be divided into two subsets A and B, such that
- subset A is all the points in S, shifted sideways a bit
- subset B is all the points in S, rotated a bit.
- it doesn't require the axiom of choice
- the infinite set it duplicates is countable
- it uses only two subsets, not five
- it's simpler to describe how it works.
S is the set of all polynomials with whole number (integer >= 0) coefficients, evaluated at q. Plot them as points on the complex plane. A few sample polynomials and their values at q:
| P(x) | P(q) |
|---|---|
| 19 | 19 |
| x + 7 | cos(1) + 7 + i sin(1) |
| x² + 3x | cos(2) + 3 cos(1) + i (sin(2) + 3 sin(1)) |
| 5x³ | 5 cos(3) + i 5 sin(3) |
Note that cos(1), sin(1), cos(2), sin(2), ... are all transcendental.
Partition S into two subsets:
- subset A contains all the points generated by polynomials with a nonzero constant term, e.g., 19 and q + 7.
- subset B contains all other points in S. They are generated by polynomials with no constant term, e.g., q² + 3q and 5q³.
Rotating the points in B clockwise by one radian (57.2957795...°) is tantamount to multiplying their values by e‑i, which reduces the exponent of each polynomial term by one. The result is all the points in S.
I don't know about you, but I think that's pretty cool.
Thanks to Dr. Francis Edward Su, on one of whose pages I found this.
To show that S is a countably infinite set, define the rank of each polynomial as its degree plus the sum of all its coefficients. E.g., the rank of x² + 3x is 2+1+3 = 6. To enumerate the polynomials with whole number coefficients,
| list the polynomial | of rank zero, | then | |
| list the polynomial | of rank one, | then | |
| list the polynomials | of rank two, | then | |
| list the polynomials | of rank three, | and so on. |
current journal
FAQ
contact
rss/xml
atom/xml
spam notice
archive
FAQ
contact
rss/xml
atom/xml
spam notice
archive
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
| jan | feb | mar |
| apr | may | jun |
| jul | aug | sep |
| oct | nov | dec |
